BQ 7: Unit V

The formula for the difference quotient is f(x+h)- f(x) divided by h. It is derived from the slope formula of y^2-y^1/x^2-X^1. The only difference is that as seen on the graph the section of x+h is substituted  in the place of y^2 and then y with x. Next its done the same with the bottom leaving it as x+h-x. Next you move on by canceling out the x's leaving the h on the bottom. So its simply substituting in the correct values into the slope formula resulting in the difference quotient. This all being shown in the image provided. The image shows how delta x can be used as another notation for the h. The purpose always being to get delta x as small as possible, making the tangent line less steep. Because the smaller the delta x, the more the secant and tangent lines resemble one another.

BQ#6: Unit U

1. What is continuity? What is discontinuity?

Continuity means that the graph is predictable. Also it has no breaks, holes, or jumps, and it can be drawn without lifting the pencil off the paper.

Point Discontinuity

Oscillating Behavior

Jump Discontinuity

Infinite Discontinuity

 

 

            Discontinuities can be seen in graphs when it has point, oscillating, jump, and infinite discontinuities. Within these discontinuities there are two groups, removable and non-removable discontinuities.  A type of removable discontinuity is a point discontinuity. This means that there's a hole in the graph(as seen in the first graph). Non-Removable discontinuities consists of jump discontinuity, oscillating behavior, and infinite discontinuity. Jump discontinuity means that if we trace the graph with our left and right finger on the graph and get to different points(third picture). It is important to know that the jump can have two open circles, one close/open, but they must never be two closed circles. Oscillating behavior is also part of non-removable discontinuities. In oscillating behavior the graph is very wiggly, or unpredictable. In this case the limit dne because you can't really cant tell where the graph's next destination will be. Infinite discontinuity is the last part of non-removable. This is when there's a vertical asymptote leading to unbounded behavior. Unbounded behavior means the graph is either going up infinitely or down infinitely (last picture)

 2. What's a limit? When does a limit exist? When does a limit DNE? What's the difference between limit and value?

                A limit is the intended height of a function. A value is the actual height of a function. A limit exists when the intended and actual height are the same (value) . A limit is the value that a function or sequence "approaches" as the input or index approaches some value. A limit does not exist when the left and right are different(jump), unbounded behavior(vertical asymptote), and oscillating behavior. 

3. How do we evaluate limits numerically, graphically, and algebraically?

To begin numerically means on a table. So with this in mind we evaluate a limit numerically by making an x and y table with seven spaces. Then we write the limit in the middle box. Afterwards we come up with the x values by adding and subtracting 1/0. Once we have that we plug in the function and trace the numbers that we have on the table (x-values). Once we plug in the limit if the calculator does not give us an answer then it is undefined. For algebraically there are three methods that can be used. The first method is substitution. In this method we just plug in the limit and solve. There are three answer that we can get which are a number, a zero divided by a number which is zero, a number divided by zero which is undefined, and 0/0 which is indeterminate form. If we get indeterminate form we have to use the dividing/factoring method or rationalizing/conjugate method. In the factoring method we have to factor the numerator and denominator and cancel like terms to remove the zero. Then with the simplified expression, use substitution to find the answer. The rationalizing/conjugate method is when you multiply the radical with its conjugate. Remember to not multiply the non-conjugate because something would hopefully cancel. Once something does cancel, you use substitution to get your answer. 

 

 Factoring Method

 

substitution method 

 

 Rationalizing Method

 

 

 

BQ #3: Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?

1. Tangent
The ratio for tangent is sin/cos. So the asymptotes are located when tangent is 0, this would only happen when cos is equal to 0. Since cos is the x-value the asymptotes are located where x=0. That would be at pi/2 and 3pi/2.  If we recall from the unit circle all trig functions in the first quadrant are positive. Both sin and cos are pos. in the first quadrant so that means that  when you divide one by the other, you end up with a positive value for tangent. For quad.2 we know that sin is positive and cosine is neg. This means we get a negative value for tangent.in the third quad. sin and cos are both negative so we get a positive value for tan. In quad 4sin is pos and cos is neg. A and get a neg. value for tangent. The graph for tangent is pos, neg, pos, neg. When we graph it within its period and based on the location of the asymptotes it will be uphill or downhill.

2. Cotangent

The trig ratio for cotangent is cos/sin. So the asymptotes are located where sin is equal to 0(y). The asymptotes would be located at 0 and 180 because y=0 there.To find out how the appearance for cotangent graphs we can use the trig ratio for cotangent looks, we can use the  trig ratio for cot (cos/sin). Sin and cos are positive in the first quadrant, so when you divide one by the other, you end up with a positive value for cot. For quadrant 2 we get a negative value for cot. For the third quadrant we get a positive value for cot. In  the fourth quadrant 4,we get a negative value. The graph for cotangent is pos, neg, pos, neg. When we graph it within its period of 0 and pi, the graph will begin close to the asymptote above the x-axis.  When it enters second quad. it will be negative so we have to draw it downhill.

https://www.desmos.com/calculator/hjts26gwst

3. Secant

Secant is the reciprocal of cosine. It has a ratio of 1/cos. Since cosine is the denominator when it equals zero we will have asymptotes. Secant has asymptotes at pi/2 and 3pi/2(keep in mind that they go on forever to the left and right). These asymptotes are the only ones within the period. If secant is positive then the graph will go upward and if its negative the graph will go downward. Also if cosine is positive or negative secant will also.

https://www.desmos.com/calculator/hjts26gwst



 4.Cosecant?

 Cosecant is the reciprocal of sine. It has a ratio of 1/sin. We get asymptotes when the denominator equals zero. Cosecant has asymptotes at 0 and pi (they keep going).If sine is positive so will the cosecant graph. Cosecant is also affected by that.

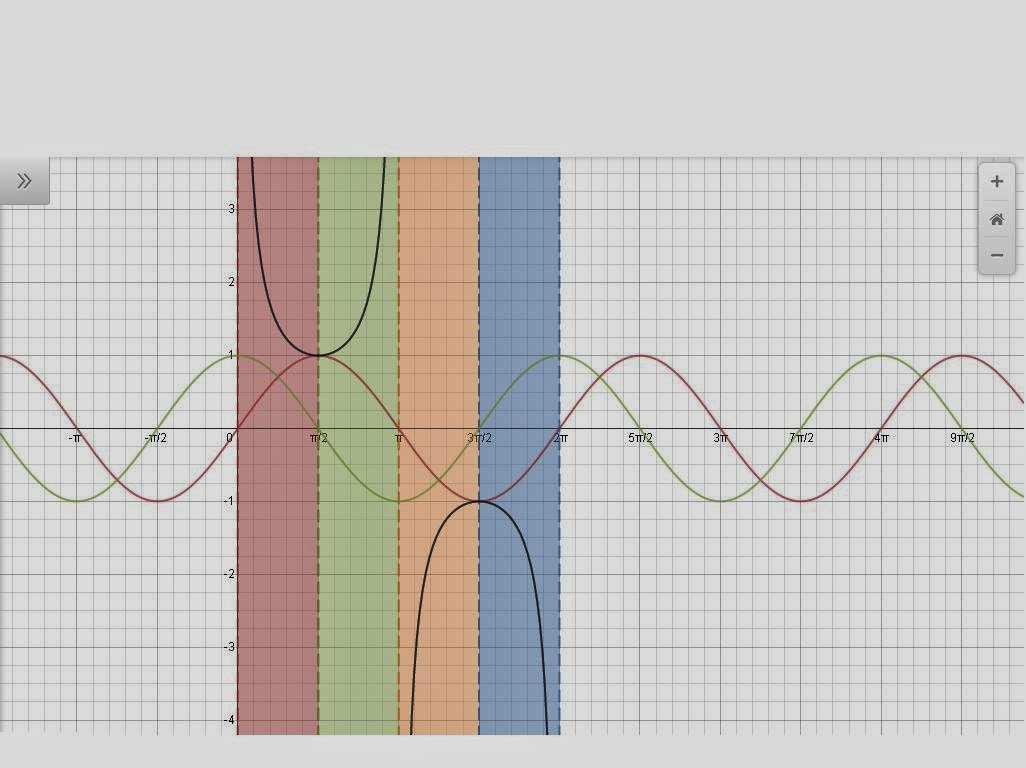https://www.desmos.com/calculator/hjts26gwst

BQ #4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill?

          The normal tangent graph is uphill mainly because of the asymptotes. One of the reasons why its uphill is because of the asymptotes which are located at pi/2 and 3pi/2 (keep in mind they go on forever). If we recall from the unit circle the first quadrant was positive, the second negative, the third positive, and the fourth negative. So if we draw our asymptotes our graph has to be in between those asymptotes so that means where in the third and second quadrant. As mentioned above the third quadrant is positive and the second one is negative. So that means our graph has to be below the x-axis and then above the x-axis.

                       The normal cotangent graph is downhill because of its asymptotes.  The asymptotes for the normal cotangent graph are pi and 0. The labeling of the quadrants is the same. So it would be above the x- axis and then below as seen below.
    

BQ#5: Unit T: Concepts 1-3

Why do sines and cosine NOT have asymptotes, but the other four trig graphs do?
            

       To begin the ratio for sine is y/r and for cosine its x/r. If we recall r is 1 so that means that r can never equal 0 so we can't get an asymptote. We cannot get an asymptote because in order to get an asymptote we have to get an undefined and we can only get an undefined when we divide by zero.  Cosecant has a ratios of r/y and cotangent has a ratio of x/y. This means that we will get asymptotes when y=0. Also the asymptotes will be in the same place. The ratios for secant (r/x) and tangent (y/x) both end with x. So we get asymptotes when x=0. All trigs, except for sine and cosine, can be divide by zero this means that we can get an undefined and have asymptotes on the graph.

BQ #2: Unit T Concept Intro

1. How do the trig graphs relate to the Unit Circle?
      

 

 

 

          The trig graphs relate to the Unit Circle because it uses the negative and positive values of the quadrants in order to define how a period/graph will look  for a certain trig function. Each trig function forms a different looking graph. To begin the unit circle unfolds into a line. As we can see above the signs in parenthesis are the values that that quadrant would have on the unit circle (positive or negative). Since we unfolded the unit circle for the sine graph we are left with positive and on the left and negative on the right. This means that our graph will look like an uphill then a down hill. For the cosine we see an uphill, downhill, and then uphill again because of the positive, negative, negative, and positive value on the quadrants when we unfolded the Unit circle. Tangent/cotangent both have an uphill and downhill because they have a shorter period due to the positive and negative on the first two quadrants and positive negative in the third and fourth quadrant.

 

       -Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

     The period for sine and cosine is 2pi because it takes four quadrants to repeat the same pattern over and over again. Tangent and cotangent has a period of pi because since it already has a positive and a negative value on the first two quadrants it only takes pi to repeat the pattern.

 

        -Amplitude? - How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?

        The fact that sine and cosine have amplitudes of one relates to what we know about the unit circle because sine and cosine cannot be bigger that one. Since sine and cosine has a ratio of y/r and x/r and r =1. Sine and cosine can only be between -1 and 1.

Reflection#1: Unit Q Concepts 1 & 5

1. To begin proving an identity is very different from solving a problem. To prove an identity, you have to use identities to show that one side of the equation can be transformed into the other side of the equation. You don't plug values into the identity to prove anything. There are several different identities you can plug in. We also have to keep in mind that we can not touch the right side when verifying.

2. One of the main tricks that I found useful were trying to maintain sin and cos in the problem. Another trick that I found helpful was knowing when to combine and break up fractions so that the number of terms will match. The last trick that I found helpful was factoring out the GCF.

3.There are several ways that we can approach a problem. However, there are several things that we can do first such as looking for a GCF, substituting an identity, multiplying by the conjugate(when the denominator is a binomial), combine fractions with binomial denominators, and factoring.


   

SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig fFunction and Quadrant

Please see my SP7, made in collaboration with Elizabeth T., by visiting their blog here.  Also be sure to check out the other awesome posts on their blog

I/D #3: Unit Q Concept 1: Using Fundamental Identities to Simplify or Verify Expressions

INQUIRY SUMMARY ACTIVITY

1. Where does sin^2x + cos^2x=1 come from?

To begin this is a Pythagorean identity. An identity is a proven fact or formula that is always true. The first thing we did was write out the Pythagorean theorem as show below. Then we replaced a^2+b^2=C^2 with x^2+y^2=r^2 ( as shown above) We are able to replace it with these variables because it consists of the same characteristic as the unit circle, were using all the variables from the first quadrant. At this moment our formula  is  x^2 + y^2 = r^2 and we want to get to sin2x+cos2x=1. To do that, we divide everything by r^2. If we divide everything by r^2, we get this: x^2/r^2 + y^2/r^2 = 1 (r^2/r^2).  So r^2/r^2 becomes 1 and we can put (x/r) ^2+ (y/r)^2=1. Then we should notice that these variables are the ratios of  cosine and sine. Now that we know this we can replace then and get a final answer of cos^2x+sin^2x=1.


Does it really work?

 

           In order to verify that it works we can plug in the 30,45 and 60 degree angles. ( All values from the unit circle) In this case I choose 60*. The 1/2^2 becomes 1/4 and the rad3/2 becomes 3/4 because the squared cancels the 3 and you just multiply 2 by 2. This gives us an answer of 1.

 

2. The other Pythagorean Identities.

 

 

 

 

 The picture above shows the steps of how to get tan^2x + 1 = sec^2x. First, you will have to divide both sides by cos^2x. For this one, we want tangent and secant. We can look at that as y/r times r/x. So as a result we have y/x which is tangent. Cosine divided by cosine is simply 1. And 1 divided by cos2x  which is sec2x because sec x = 1/cos x, we just powered up because everything is being multiplied in this reciprocal identity. (look at the picture above)

 

The other Pythagorean identity is 1+cot^2x=csc^2x. In this identity we have cot and csc.  We divide everything by sin2x . We divide cos^2x by sin^2x and we get cot^2x. We divide 1 by sin^2x and we end up with csc2x. This is how we get the answer.

 

INQUIRY ACTIVITY REFLECTION 

1.THE CONNECTIONS I SEE WITH UNIT N, O, P AND Q SO FAR ARE the trig functions and the ratios. Also the magic three from the unit circle to derive the things above.

2. IF I HAD TO DESCRIBE TRIGONOMETRY IN THREE WORDS, THEY WOULD BE sin, cos, and tan.

 





WPP #13-14: Unit P Concept 6 & 7: Applications with Law of Sines and Cosines

Please see my WPP13-14, made in collaboration with Ismael R., by visiting their blog here.  Also be sure to check out the other awesome posts on their blog”

BQ #1: Unit P Concept 3 and 4: Law of Sines and Area of an Oblique Triangle

Law Of Sines:

       1. Law of Sines - Why do we need it?  How is it derived from what we already know?  

           

           We use the law of sines when we don't have a right triangle. In previous concepts we were able to use the Pythagorean Theorem but were not able to use it in this concept because  we are not dealing with right triangles. .Also like in the unit circle the restriction for sine is still applied (it can't be bigger than one). It is very important that you know that this law can only be used when we have ASA or AAS. The Law of Sines can be used when it comes to non-right triangles with AAS and ASA. This law was derived from a non-right angle triangle. To begin we drew a perpendicular line from the top of the triangle to the bottom and labeled  that "h." Now that we have the two triangles the next step is to take the sin of A and C ( opposite/ hypotenuse). The next thing that we have to do is get h by itself so what we do is multiply both sides by its denominators as shown in the picture. In addition since both equations equal h we can set them equal to each other and we try to get sin by itself on top. So we obtain an answer of sinA/a= sinC/c.


Area of an Oblique Triangle:

1. How is the "area of an oblique" triangle derived?

 

 

(http://www.compuhigh.com/demo/lesson07_files/oblique.gif)



 

The area of an oblique triangle is derived from the original area formula for triangles (A=1/2bh). Since the perpendicular line of the triangle is the height(h) and b is the base. While the oblique triangles area is one half of the product of two sides and the sine of their interior angle.

We know that sinC=h/a from previous concepts, so once you multiply 'a' on both sides h=a sin C, and plugging 'h' into that A=1/2bh formula we really have A=1/2b(a sin C).

 

How does it relate to the area formula you are familiar with?

It relates to the area formula were familiar with  because there very similar the only difference is that h is replaced by the sin of the included angle. Another thing that we used that we had used in the past was SOHCAHTOA.

WPP #12: Unit O Concept 10: Solving angle of elevation and depression word problems

Create your own Playlist on LessonPaths!

I/D #2: Unit O - How can we derive the patterns for our special rights triangle?

INQUIRY ACTIVITY SUMMARY:

1. 
   

    

    

30-60-90 Triangle:        To begin we have to know that it is an equilateral triangle. This means that all sides and angles are equal. With that in mind we realize that the triangle has three angles, and all the angles in a triangle add up to 180 so what we do is divide 180 by 3 and get an answer of 60.
Then we cut straight down on the triangle and that gives us an angle of 30* on the top because since we divide it symmetrically the angle dives into two. If we were to add 30+30 we would get an answer of 60.  Then we created a 90* angle on the bottom left because the line created a perpendicular angle with the bottom of the triangle. ( as shown in the first picture). Since its an equilateral angle we know that all sides are equal and in this case it has a measurement of 1 on all three sides. The bottom side is 1/2 because its half of one. To find the other side (height) we use the Pythagorean Theorem ( a^2+b^2=c^2). We plug in 1/2 for a, were looking for b, and we plug in for 1 for c. This gives us an answer of rad3/2 for b. However to make the sides easier do deal with we give all sides  a variable, we will use n, and were going to give that n a value of 2n. We give it a value of two because we don't want to deal with fractions. (see picture 2) Once we have done that we get a hypotenuse of 2n a horizontal side of n, and a vertical side of n rad3. Remember n just represents any number and it keeps the relationship consistent.

    2. 45-45-90 triangle

             For the 45-45-90 triangle we begin with a square. A square has four equal sides and four 90* angles.  (see the first picture)First we drew a diagonal which  cut the 90* angle into two  pieces and that left us with  a 45 degree angle. Since all sides are equal the horizontal and the vertical sides are 1. Then we use the Pythagorean theorem to find c ( diagonal). We use 1 for a and b and that gives us an answer of rad2 (picture number 2)  Then we add n because n represents any number and it remains the relationship consistent.

INQUIRY ACTIVITY REFLECTION
       1. Something I never noticed before about right triangles is how we were able to find the ratios from the equilateral triangle and a square.
        2. Being able to derive these triangles myself aids in my learning because  I can understand how a special right triangle works and use this for concepts 7 and 8.

I/D# 1: Unit N Concept 7: The Unit Circle

• INQUIRY ACTIVITY SUMMARY

                 1.        Describe the 30* triangle:
                                  

              The first thing I did was label the triangle according to the Special Right Triangle. The hypotenuse was labeled as 2x, the horizontal side x rad3, and the vertical x.  Next we had to simplify the hypotenuse to make it one. In order to do that we had to divide all three sides by 2x. As seen in the picture above we can see that when we divided x by 2x the x's canceled and it became 1/2. For the horizontal side the x's also canceled and it simplified to rad 3/2.  Afterwards, I labeled the hypotenuse r, the horizontal value x, and the vertical value y. Then I drew a coordinate plane. We began by making the labeled angle side the origin (0,0). Then near the 90 angle I labeled it as ( rad3/2,0) because we moved rad 3/2 on the x axis and we didn't move any units up. The top vertices is labeled as ( rad3 /2,1/2) because we moved right rad3/2 and up 1/2.

                2. Describe the 45* Triangle:
                          

 

 

               The first thing I did was label the triangle using the rules of Special Right Triangle. For this triangle the hypotenuse is x rad 2 and the horizontal and vertical side are both x. Then we had to make the hypotenuse 1. In order to do this we had to divided xrad2 by xrad2(hypotenuse) to obtain an answer of one. Then I have to divide the two other sides by xrad2 and since both are x, when we divide by xrad2, we get rad2/2. However, sine there is a square root in the bottom we had to simplify. The next step was to label the hypotenuse r, the horizontal value x and the vertical value y. Afterwards we also had to draw a coordinate plane. We also labeled the origin at the given labeled angle (0,0). As showed in the second triangle, we labeled the 90* vertex (rad2/2,0) because we moved rad2/2 along the x- axis and 0 unit along the y axis. Finally for the top vertex the point would be (rad2/2,rad2/2 because we moved along the x and y axis rad2/2. 

               3.  Describe the 60* triangle:

 

                                          

 

                  This is very similar to the 30* triangle but for the 60* triangle the sides are switched. The hypotenuse still being 2x, the vertical side x radical 3, and the horizontal side as x. We first divide everything by 2x and we get a vertical side of radical 3/2, a horizontal side of 1/2, and hypotenuse of one (just like the 30* angle and after simplifying).Next we place the triangle on the first quadrant giving us ordered pairs of (1/2, radical 3\2), (1/2,0), and (0,0). 

 

            4. This activity helps me derive the unit circle because it gives me the degrees, points, and ordered pairs that are located at quadrant one of the unit circle. These three triangles are important because there reflected on the unit circle. The vertices on the top are the points used all around the circle but they have different x and y values. ( explained below)

 

 

 

 

 

             5.  The 30*,45*,and 60* triangles that we did in the activity lie on the first quadrant. Since the first quadrant is reflected on the second quadrant, the second is reflected on the third quadrant,  and the third on the fourth quadrant. The values of the vertices change. In the first quadrant both values are positive, in the second quadrant the x value is negative. In the third quadrant the values of both the x and y are negative. For the fourth quadrant the y value is negative.

 

INQUIRY ACTIVITY REFLECTION

The coolest thing I learned from this activity was how the triangles even when shifted to different quadrants are the same as the first quadrant.

 

This activity will help me in this unit because with just knowing the ordered pairs from these three triangles, I can easily narrow down the answers for degrees that have the share reference angles.

Something I never realized before about special right triangles and the unit circle is that I can see the unit circle as triangle to find the vertices.